

Propiedad Intelectual de Dr. José VERGARA, Ingeniero Civil, Ph.D. (Ciencias),
email: DrJoseVergara@yahoo.com
En mis dos artículos anterior, se demostró que la ley que siguieron los contagios por COVID-19 en Chile, es la ecuación exponencial por tramos.
Donde C(t) son los contagios observados después de un tiempo t (días) y To es la escala de tiempo, inicial fue 2,9 días, esta ley explicó la evolución de los contagios durante las primeras tres semanas de la epidemia y donde alcanzaron los 500 casos.
Durante esta etapa cada 7 días el número de Infectados se amplificaba por 10 (Figura 1).
La Figura 1 muestra claramente dos quiebres en la curva de crecimiento del número de casos confirmados: durante los días 22 y 29 de marzo, dos fechas en las que se tomaron medidas más severas, lo que permitió bajar la tasa de crecimiento a la mitad (To= 5,4 días) comparable a Canadá y durante la última semana a 9,4 días, hoy:
Casos COVID-19 confirmados nacionales se incrementan X 10 cada 21 días (tres semanas).
Nota un To mayor significa un crecimiento más lento de la epidemia y por lo tanto mayor tiempo para que la autoridad y comunidad pueda reaccionar.
Que ocurre en el Aconcagua, como se observa en la Figura 2, la evolución es similar a lo observado durante las ultimas dos semanas a nivel nacional, la curva del Aconcagua muestra una clara disminución en su tasa de crecimiento y al día de hoy 4 de abril, el tiempo para incrementar los casos en 2,7 veces es de 7,4 días, con una evolución más lenta. Lo que muestras que las acciones tomadas tanto por autoridades, como por la comunidad en general están en el camino correcto.
Por lo que la curva de casos confirmados en el Aconcagua se está aplanando, y es de esperar que con nuevas medidas especialmente a nivel comunal, la aplanen más.
De mantener las acciones actuales, el número de casos confirmados llegaría a 500 casos durante el fin de semana próximo.
Articulos Anteriores
https://www.reeditor.com/columna/22940/4/biologia/las/leyes/coronavirus/o/covid19/chile/espana
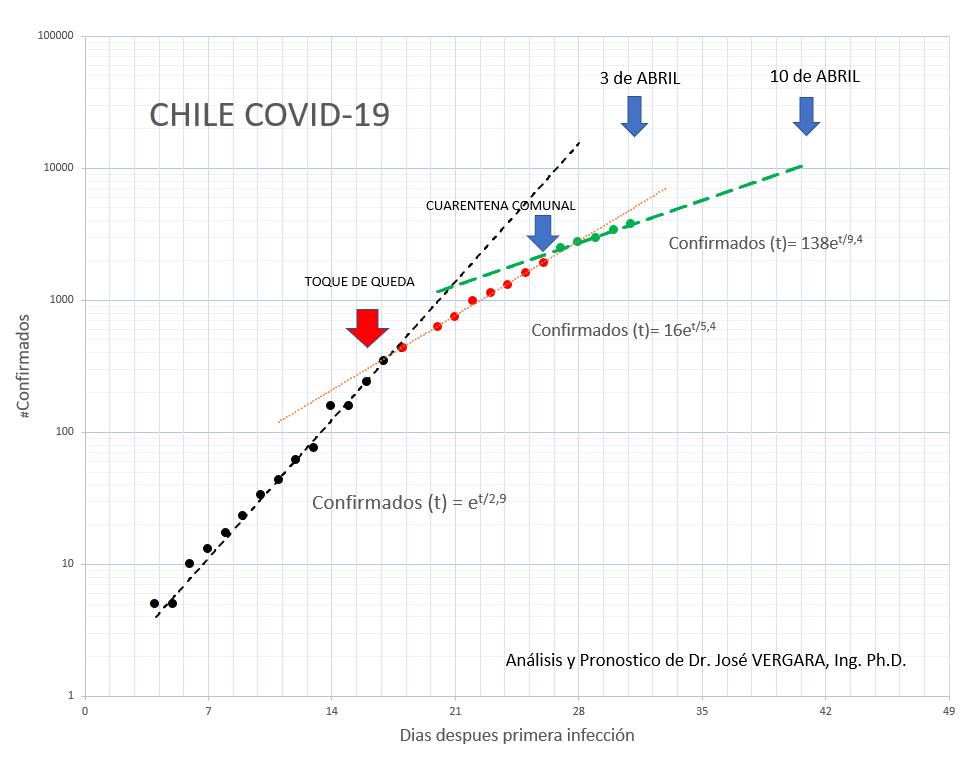
Figura 1: Evolución temporal del número de infectados en Chile por COVID-19. Durante los últimos 30 días. En las primeras dos semanas el número de infectados creció según un desarrollo exponencial, incrementándose los contagiados por un factor de 2,7 veces cada 2,9 días similar a España. Pero dada la preocupación que esto género, las autoridades y comunidad en general tomaron acciones incrementales: Durante la tercera semana se instauró el Toque de Queda, se suspendieron las clases y se restringieron las reuniones, lo que se reflejó en una reducción significativa en la tasa de incremento de 2,7 veces cada 5,4 días, un valor que es comparable con Canadá, mientras que durante la última semana se implementaron medidas adicional con cuarentena comunal en las zonas más afectadas, barreras sanitarias y sanitización generalizada de espacios públicos, esto nuevamente se reflejó en una nueva reducción en la tasa de crecimiento quedando al día de hoy el tiempo de amplificación de 2,7 veces en 9,4 d. Por lo que el umbral de 10.000 casos confirmados se extiende al próximo fin de semana, lo que es una muy buena noticia. La curva logística se está aplanando.
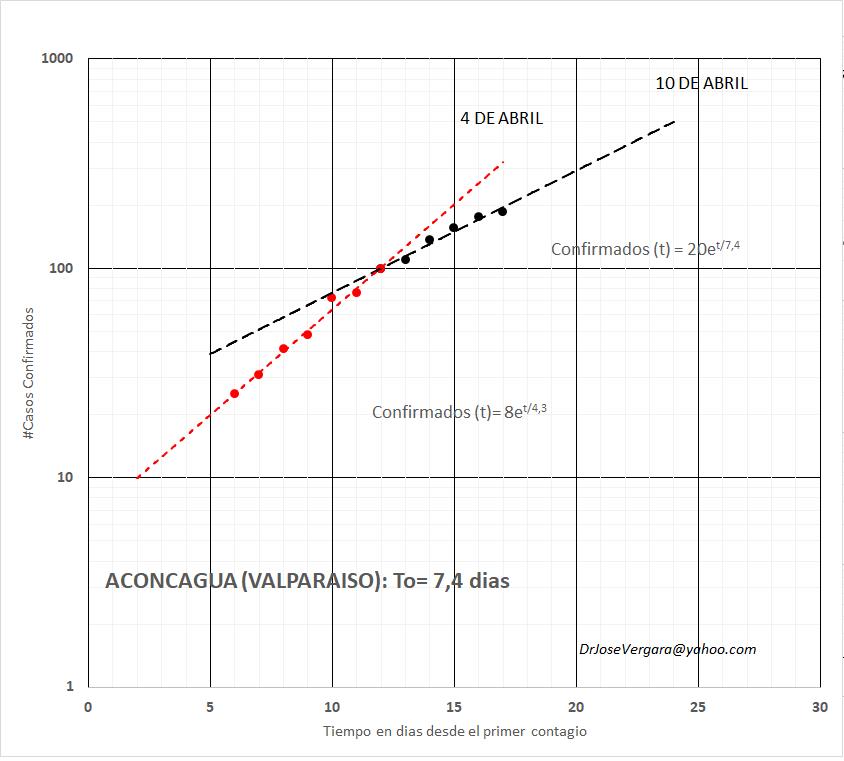
Figura 2: Evolución temporal del número de infectados en el Aconcagua por COVID-19. Durante los últimos 20 días. En las primeras dos semanas el número de infectados creció según un desarrollo exponencial, el que se ve modificado por las distintas acciones tomadas, tanto por la autoridad nacional, local y comunidad en general. Hoy la tasa de crecimiento se amplifica en un facto de 10 cada dos semanas, con un pronóstico para Semana Santa de 500 casos.
Dr. Jose VERGARA, Ph.D. (DrJoseVergara@yahoo.com)















